机器学习：无监督学习

无监督学习

1 基本概念

聚类通常被称为无监督学习，其是一种发现数据中的相似群体的技术，解决的是未知类别的训练样本预测问题。由于历史的原因，聚类和无监督学习的关系更加紧密，因此被广泛认为是相同的概念。事实上，关联规则挖掘也是无监督学习。

所谓聚类就是将对物理或抽象对象的集合分组，依据在某些方面类似的数据对象进行划分簇的过程。

聚类生成的组称为簇，簇是数据对象的集合

簇内部任意两个对象之间有较高的相似度；
属于不同簇的两个对象之间具有较高的相异度；

聚类既能作为一个单独过程，用于找寻数据内在的分布结构，也可作为分类等其他学习任务的前驱过程。

基于不同的学习策略，大体上，主要的聚类算法可以分为如下五类：

基于划分的方法；
基于层次的方法；
基于密度的方法；
基于网格的方法；
基于模型的方法；

评价一个聚类方法的好坏，一般对类内差异和类间差异进行评价。聚类结果的质量与表示，算法，距离函数和应用领域有很大关系。

2 K-Means

K-Means（K-均值）算法是一种基于划分的聚类算法。它根据某个距离函数反复地把数据分入K个聚类簇中。其中K是由用户指定的

基于划分的聚类算法：就是采用目标函数最小化的策略，通过迭代把数据对象划分成 k 个组，每个组为一个簇。

K-Means 算法的执行步骤：

随机选取 K 个数据点作为 初始聚类中心；
计算每个数据点与各个中心之间的距离，把每个数据点分配给距离它最近的聚类中心；
分配完成后，根据每个聚类簇内的数据重新计算该聚类中心；
不断重复上述过程，直到 迭代次数达到要求 / 重新计算后的聚类中心偏移量小于指定阈值 / 数据点的分配结果不再变化 / 误差平方和局部最小；

误差平方和：Sum of Squared Error, SSE

$SSE=\sum\limits^k_{j=1}\sum\limits_{x\in Cluster_j}distance(x,m_j)^2$

其中， $Cluster_j$ 表示第 $j$ 个聚类簇， $m_j$ 是其中心。

K-Means 的优势

易于理解；
高效：时间复杂度为 $O(tkn)$ ，其中 $t$ 是循环次数， $k$ 是聚类个数， $n$ 是数据点个数；

K-Means 的劣势

只能用于均值可被定义的数据集上；
需要先指定一个聚类数目 $k$ ；
算法对噪声敏感；
算法对初始聚类中心敏感；
不适合发现形状不是超维椭圆体或球体的聚类；

解决异常值的方法

在聚类过程中去除离群点，或使用随机采样方法——先在部分数据点上预先聚类，再将所有的数据点分配给这些聚类。

3 聚类的表示

聚类中心表示法：用聚类中心表示每个聚类簇，计算聚类簇的半径和标准差来确定聚类在各个维度上的伸展度。适用于高位球体形状的聚类。

分类模型表示法：将同一聚类中的样本点看作同一类别，运用其他分类方法来在聚类结果上发现分类模型。

常见值表示：利用聚类中最为常见的值来表示聚类。

4 层次聚类

层次聚类试图在不同层次对数据集进行划分，从而形成树形的聚类结构。层次聚类有自下而上/自上而下的两种方法。

自下而上：从树状图的最底层开始构建聚类树，将每个样本看作一个初始聚类簇。不断地合并最相似的两个聚类簇，形成上一层中的聚类，直到所有数据点都在同一个聚类中（Root）。

自上而下：从一个包含全部数据点的数据开始分裂，直到出现只包含一个数据点的聚类时停止。

合并聚类（自下而上）被使用的更加广泛。

两个簇类之间的距离计算：

单链接方法：两个聚类簇之间的距离是两个聚类簇中最近的两个数据点之间的距离。该方法适合寻找形状怪异的聚类，但对噪声（离群点）敏感；
全链接方法：两个聚类簇之间的距离是两个聚类中所有数据点之间距离的最大值。对噪声敏感；
平均链接方法：两个聚类簇之间的距离是两个聚类簇之中多个数据点对之间距离之和的平均值；
聚类中心方法：两个聚类簇之间的距离是两个聚类簇中心之间的距离；

层次聚类算法的计算复杂度至少为 $n^2$ ，在处理大规模数据时十分低效。

5 距离函数

5.1 数值属性之间的距离

最常用的距离函数是欧几里得距离和曼哈顿距离，这两种距离函数都是闵可夫斯基距离的特殊情况。

闵可夫斯基距离：Minkowski Distance

$Minkowski\_Distance(x_i,x_j)=(\sum\limits^{d}_{k=1}|x_{ik}-x_{jk}|^p)^{\frac{1}{p}}$

$p$ 一般是整数。当 $p=1$ 时，表示曼哈顿距离；当 $p=2$ 时，表示欧几里得距离。

加权欧几里得距离：

$dist(x_i,x_j)=\sqrt{\omega_1(x_{i1}-x_{j1})^2+\omega_2(x_{i2}-x_{j2})^2+...\omega_d(x_{id}-x_{jd})^2}$

平方欧几里得距离：加大了距离较远的数据点的权重。

$dist(x_i,x_j)=(x_{i1}-x_{j1})^2+(x_{i2}-x_{j2})^2+...(x_{id}-x_{jd})^2$

切比雪夫距离：

$dist(x_i,x_j)=max(|x_{i1}-x_{j1}|,|x_{i2}-x_{j2}|,...|x_{id}-x_{jd}|)$

5.2 布尔属性之间的距离

混淆矩阵：

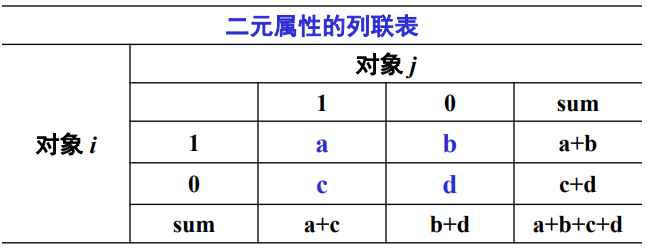
当布尔属性的两个状态具有相同的重要性并且具有相同的权重时，我们称这个布尔属性是对称的。对称属性中使用普遍的距离函数简单匹配距离（Simple Matching Coefficient），是指属性中值不匹配的属性的比例：

$dist(x_i,x_j)=\frac{b+c}{a+b+c+d}$

当布尔属性的一个状态比其他状态更重要时，我们称这个布尔属性是非对称的。通常用1表示那个更为重要的状态，即出现的较少或不太频繁的状态。非对称属性中使用最多的距离度量函数是 Jaccard距离（Jaccard coefficient）：

$dist(x_i,x_j)=\frac{b+c}{a+b+c}$

5.3 符号属性之间的距离

类似于布尔属性的距离，符号属性的距离度量函数也是基于简单匹配距离的：

$dist(x_i,x_j)=\frac{d-q}{d},\ 其中d为属性的数目，q为属性值匹配的数目$

5.4 文本文档之间的距离

文本文档是由一系列由单词序列组成的句子组成的，因此，文档可以和普通数据点一样用向量来表示。比较两个文档时，通常计算的是两个文档的相似度而不是它们的距离，使用最多的相似度函数是向量夹角余弦相似度（cosine similarity）：

$cos(\theta)=\frac{\sum\limits^d_{i=1}(x_i\times y_i)}{\sqrt{\sum\limits^d_{i=1}(x_i)^2}\times\sqrt{\sum\limits^d_{i=1}(y_i^2)}}$

6 数据标准化

在使用欧几里得距离时，为了使数据中的各个属性在距离计算过程中具有相同的作用，对数据进行标准化处理。

标准化属性：强制各个属性都在一个相同的范围内变化。

6.1 区间度量属性

指符合线性标量的实数值。两种主要的标准化方法是范围标准化和z-score标准化。

范围标准化：

$range(x_i)=\frac{x_i-min_f(x_if)}{min_f(x_if)-min_f(x_if)}$

z-score 标准化：基于属性的平均值和标准差来对属性进行标准化。z-score 标准化数值指出的是属性值从哪个方向远离属性均值以及偏离属性均值的距离。计算公式如下：

$m_f=\frac 1 n (x_{1f}+x_{2f}+...+x_{nf})\\ s_f=\frac 1 n (|x_{1f}-m_f|+|x_{2f}-m_f|+...+|x_{nf}-m_f|)\\ z_score(x_if)=\frac {x_{if}-m_f} {s_f}$

6.2 比例度量属性

非线性的数值属性。可使用对数函数转换后，再进行区间度量属性的标准化方法。

6.3 符号属性

将符号属性转换为布尔属性：

某个符号属性的属性值个数为v
建立v个布尔属性分别表示它们
当一个数据实例的该符号属性取了一个特定的属性值时，我们就把该属性值对应的布尔属性的属性值取为1,其余的取0

本质上是 One-hot 编码。

6.4 顺序属性

常用的标准化方法是将顺序属性看作区间度量属性，以进行标准化。

6.5 混合属性的处理

转换成一个类型：先在混合属性中确定一个属性类型作为主导类型，然后把数据集中的其他类型的属性转换成该数据类型。

合并距离：首先分别根据各个不同类型的属性计算两个数据点之间的距离，然后把这些不同属性的距离结合起来得到一个最终距离。

7 聚类算法的选择

执行不同的算法，使用不同的距离函数和不同的参数设置，比较最终结果。

结果的理解需要同时建立在对原始数据的深刻理解和对于所使用的算法的认识之上。

8 聚类的评估

8.1 基于外部信息的聚类评估

使用分类数据集来评估聚类算法。

熵：对于每个聚类，可以按下列方法计算它的熵。

$entropy(D_i)=-\sum\limits^k_{j=1}Pr_i(c_j)log_2Pr_i(c_j)$

其中， $Pr_i(c_j)$ 是聚类 $i$ 或 $D_i$ 中属于类别 $c_j$ 的数据点所占的比例。整个聚类结果的熵总和为：

$entropy(D)=\sum\limits^k_{i=1}\frac{|D_i|}{|D|}\times entropy(D_i)$

纯度：衡量一个聚类中仅包含一个类别的数据的程度。

$purity(D_i)=max_j(Pr_i(c_j))$

整个聚类结果的纯度总和为

$purity(D)=\sum\limits^k_{i=1}\frac{|D_i|}{|D|}\times purity(D_i)$

8.2 基于内部信息的聚类评估

聚类内紧密度：数据点和聚类中心的相似度。通常使用 SSE 测量。

聚类间分离度：不同的聚类中心之间的差异度。